Gyroelongated triangular cupola
| Gyroelongated triangular cupola | |
|---|---|
| Type | Johnson J21 - J22 - J23 |
| Faces | 1+3.3+6 triangles 3 squares 1 hexagon |
| Edges | 33 |
| Vertices | 15 |
| Vertex configuration | 3(3.4.3.4) 2.3(32.6) 6(34.4) |
| Symmetry group | C3v |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
In geometry, the gyroelongated triangular cupola is one of the Johnson solids (J22). As the name suggests, it can be constructed by gyroelongating a triangular cupola (J3) by attaching a hexagonal antiprism to its base. It can also be seen as a gyroelongated triangular bicupola (J44) with one triangular cupola removed. Like all cupolae, the base polygon has twice as many sides as the top (in this case, the bottom polygon is a hexagon because the top is a triangle).
The 92 Johnson solids were named and described by Norman Johnson in 1966.
Contents |
Formulae
The following formulae for volume and surface area can be used if all faces are regular, with edge length a:[1]
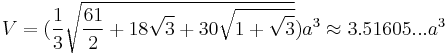
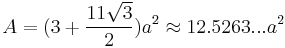
Dual polyhedron
The dual of the gyroelongated triangular cupola has 15 faces: 6 kites, 3 rhombi, and 6 quadrilaterals.
| Dual gyroelongated triangular cupola | Net of dual |
|---|---|
References
- ^ Stephen Wolfram, "Gyroelongated triangular cupola" from Wolfram Alpha. Retrieved July 22, 2010.